Unidirectional Kirman's model
Bass diffusion model [1] is widely known and very important model in marketing science. This model predicts diffusion, sales, of new successful products inside the market. While previously discussed model, Kirman model [2], has wide range of possible applications - from biology to finance. In [2] it is noted that behavior observed by entomologists is similar to one observed in economic scenarios (ex. popularity of books and restaurants). Thus one might expect that Kirman's model might be modified to work in the marketing scenario.
Bass diffusion model as a special case of Kirman's model
Bass diffusion model is underlied by the assumption that "the probability of adopting by those who have not yet adopted is a linear function of those who had previously adopted" [1]. Or mathematically:
\begin{equation} \partial_t F(t) = [1-F(t)] [p + q F(t)] , \label{bassode} \end{equation}
where \( F(t) \) is fraction of market that have adopted product by time t, \( p \) is coefficient of innovation, while \( q \) is coefficient of imitation. Solution of the above ordinary differential equation, with boundary condition \( F(0)=0 \), is:
\begin{equation} F(t) = \frac{p \left[ e^{(p+q) t} -1 \right]}{e^{(p+q)t}+q} . \end{equation}
Number of new consumers per unit of time is given by the derivative of the above:
\begin{equation} \Delta F(t) = \frac{p (p+q)^2 e^{(p+q) t}}{\left[pe^{(p+q) t}+q \right]^2} . \end{equation}
Kirman's model [2] is based on very similar ideas - some ants discover food sources independently, while other ants imitate behavior. The only difference is that in Kirman model transitions are bidirectional, while in Bass diffusion model there is only one possible transition - from potential consumer to consumer.
Though it is rather easy to introduce this unidirectionality into Kirman's model. We simply one transition probability to zero:
\begin{equation} p(X \rightarrow X+1) = (N - X) \left( \sigma + \frac{h X}{N} \right) \Delta t , \end{equation}
\begin{equation} p(X \rightarrow X-1) = 0 , \end{equation}
here \( X \) is number of consumers, while \( N-X \) is thus a number of potential consumers. \( \sigma \) and \( h \) are probabilities of individual decision and influenced decision to buy product (they should be equivalent to \( p \) and \( q \) in \eqref{bassode}). Note that transition probabilities are somewhat different from the original ones [2] (or see this model on Physics of Risk). This happens due to assumption that rate of consumption is indepedent of absolute size of the market.
By introducing continuous system state variable \( x=X/N \) (we assume \( N \) to be large enough to secure continuity of \( x \)) and by using one step formalism [3] we obtain macroscopic model for the unidirectional Kirman model,
\begin{equation} \partial_t x = (1-x) (\sigma + h x) , \end{equation}
which is notably identical to the Bass diffusion model. Thus in the limit of large \( N \) we can expect that unidirectional agent-based Kirman's model will provide similar results to the differential Bass diffusion model.
Comparison of models
Below, in Fig. 1, you can see that agreement between Kirman's and Bass diffusion models improve with larger \( N \) and \( \Delta t \) (here it is time series discretization step). With lower values of these parameters agreement is worse, as Bass diffusion model describe mean, while unidirectional Kirman's model provides only single realization. This figure is featured in [4].
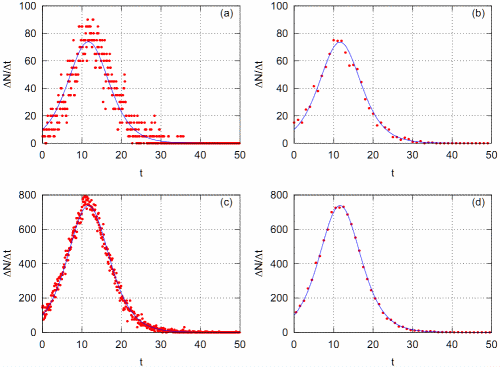 Fig 1.Agreement between Kirman's (red dots) and Bass diffusion (blue curves) models. (a) N=1000, Δt=0.1, (b) N=1000, Δt=1, (c) N=10000, Δt=0.1, (d) N=10000, Δt=1. Other model parameters: σ=0.01, h=0.275.
Fig 1.Agreement between Kirman's (red dots) and Bass diffusion (blue curves) models. (a) N=1000, Δt=0.1, (b) N=1000, Δt=1, (c) N=10000, Δt=0.1, (d) N=10000, Δt=1. Other model parameters: σ=0.01, h=0.275.Applet
This applet plots theoretical Bass diffusion curves, number of consumer and number of new consumers per unit of time, (blue continuous curves) and analogous quantities obtained from agent-based Kirman's model (red dots). Applet control parameters are identical to Kirman's model parameters with a notable exception to \( \Delta t \). Here \( \Delta t \) is time series discretization step. Kirman's model's \( \Delta t \) is selected by applet on its own. The applet also includes additional parameters \( \alpha \) (tolerance for piracy) and \( Y_0 \) (charity) not discussed in this text, but considered in the another one (Bass curves are plotted while not taking these into account).
References
- F. M. Bass. A New Product Growth Model for Consumer Durables. Management Science 15: 215-227 (1969).
- A. P. Kirman. Ants, rationality and recruitment. Quarterly Journal of Economics 108: 137-156 (1993).
- N. G. van Kampen. Stochastic process in Physics and Chemistry. North Holland, Amsterdam, 2007.
- V. Daniunas, V. Gontis, A. Kononovicius. Agent-based versus macroscopic modeling of competition and business processes in economics. ICCGI 2011, The Sixth International Multi-Conference on Computing in the Global Information Technology, pp. 84-88. Luxembourg, 2011. Note: Received IARIA Best Paper Award (see https://www.iaria.org/conferences2011/AwardsICCGI11.html). thinkmind: iccgi_2011_4_40_10188. arXiv: 1104.2895 [physics.soc-ph].
